I work on the development of interpretable and scalable methods and software for the analysis of spatial data, with applications to ecology, environmental sciences, remote sensing, as well as “omics” multiplexed imaging data. I am primarily interested in three main areas: (1) methods development for spatial multivariate data; (2) scientific applications of Bayesian methods for large scale spatial/imaging data; (3) open-source software development.
1. Methods
Multivariate data with spatial coordinates arise in situations where we observe more than one variable at many locations in a spatial domain (e.g., a portion of Earth, a human tissue, or any situation where there are x and y coordinates). In these settings, there is a trade-off between simplicity and realism: a realistic model accounts for all possible sources of statistical dependence in the data, but it is likely not very interpretable or simple to compute. My job is to create statistical models that strike a good balance between realism and simplicity. I am motivated in developing models that aptly deal with multivariate spatial dependence in the data while retaining a high degree of scalability and interpretability.
2. Applications
My interests in collaborative research include applications of Bayesian methods to cancer and environmental research. I am particularly motivated by extending the application areas of statistical ecology models to cancer imaging data to characterize disease development, progression, and treatment response.
3. Software
I have a strong motivation to make my generally-applicable methods and applications accessible and reproducible. I primarily develop my statistical software in C++ for efficient computations, and publish it in the form of R packages.
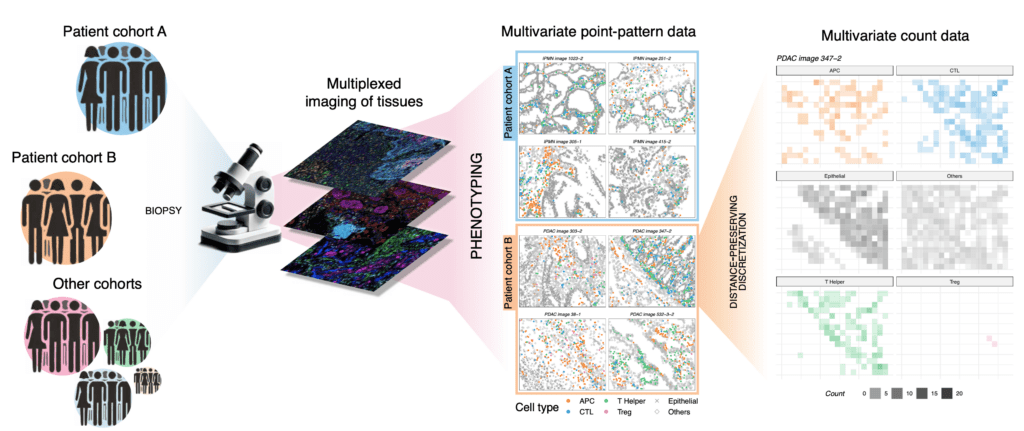
Multiplexed-imaging of tissues from multiple patients lead to large-scale datasets with complex spatial dependence. Bayesian methods for multivariate spatial data can be extended to account for patient heterogeneity and understand how disease shapes the Tumor Microenvironment (TME).
My latest methodological work is the development of a new cross-covariance matrix function — a mathematical model for how the covariance between two random vectors changes in the spatial domain. These kinds of models are the backbone for all models of multivariate spatial data, but there is a surprising lack of flexible and interpretable alternatives in the literature. While the most popular model of cross-covariance is simpler to construct mathematically, it also does not lead to interpretable inference. My contribution is a novel method that resolves many of the shortcomings of popular methods while being scalable to large datasets and highly interpretable.
I have also recently worked on applying multivariate geostatistical methods to multi-subject data from several cohorts of cancer patients. The key advantage in our novel approach is that information is pooled across subjects, leading to interpretable inference about how different cancers impact the spatial structure of tissues, i.e., the joint spatial patterns of cells in the tumor microenvironment. Downstream applications will be able to further characterize disease development and treatment response.
I would like to make tangible progress in learning about cancer. I would like my interpretable methods and software to be clinically useful and provide novel insight to cancer researchers, guiding their treatment and research strategies to ultimately make cancer a thing of the past.
